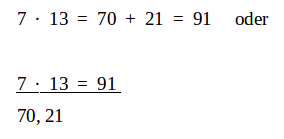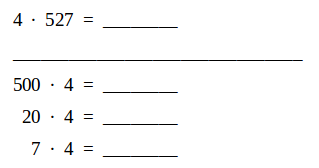Halbschriftliches Multiplizieren
Aufgaben und Übungen für Mathematik: Die Halbschriftliche Multiplikation
Voraussetzungen?Strategien zum Lösen von Aufgaben aus dem großen Einmaleins
Bezug zum Lehrplan
Zu den Aufgabenblättern
Strategien zum Lösen von Aufgaben aus dem großen Einmaleins
Bezug zum Lehrplan
Zu den Aufgabenblättern
Voraussetzungen für das Lösen der Aufgaben
Die sichere Anwendung des Einmaleins ist die Voraussetzung für das halbschriftliche Multiplizieren. Zu Beginn des dritten Schuljahres haben die Schülerinnen und Schüler die Einmaleinsreihen gelernt und automatisiert, d.h. dass sie die Aufgaben sicher im Kopf lösen können. An dieser Stelle soll noch einmal auf die Bedeutung des Kopfrechnens zur Alltagsbewältigung hingewiesen werden.Ganz im Gegensatz zum kleinen Einmaleins müssen die Kinder die Aufgaben des großen Einmaleins ( 1⋅11, 1⋅12,...bis 20⋅20, siehe Einmaleinsreihen großes Einmaleins) nicht auswendig lernen. Es müssen vielmehr Strategien zum Lösen der Aufgaben entdeckt und angewendet werden.
Von großer Bedeutung ist das Multiplizieren von Zehnerzahlen. Es ist unbedingte Voraussetzung für das halbschriftliche Verfahren. Die Einsicht in den Stellenwertbegriff und ein Verständnis des Malnehmens mit der Null sind notwendig, um halbschriftliche Multiplikationsaufgaben zu lösen.
Strategien zum Lösen von Aufgaben aus dem großen Einmaleins
Die gebräuchlichste Strategie ist die Anwendung des Verteilungsgesetzes ( Distributivgesetz ).Beispielaufgabe: 7 ⋅ 13
Drei Schritte sind bei der Bearbeitung dieser Aufgabe nötig:
- Zerlegen der Zahl 13 in Zehner und Einer: 13 = 10 + 3
- Multiplizieren jeder Zahl: 7 ⋅ 10 + 7 ⋅ 3
- Addieren der Teilergebnisse: 70 + 21
Die Notation erfolgt meist in drei Schritten. Die Lösung wird am Ende in der Leerstelle der ersten Zeile notiert.
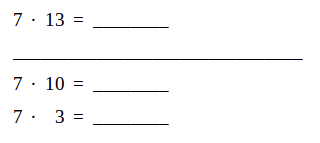
Es sind auch Kurzformen bei der Notation möglich:
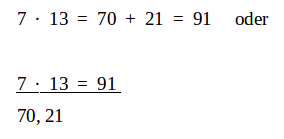
Natürlich gibt es nicht nur einen vorgeschriebenen verbindlichen Lösungsweg.
Auch andere Zerlegungen sind möglich, z.B.
5 ⋅ 13 + 2 ⋅ 13Wichtig ist, dass die gewählte Methode vom Kind beherrscht und richtig angewendet wird.
oder:
10 ⋅ 13 - 3 ⋅ 13
Wenn die Kinder die Rechenstrategien des großen Einmaleins verstanden haben, können sie diese mühelos beim Multiplizieren anderer zweistelliger Zahlen anwenden, z.B. 6 ⋅ 72; 8 ⋅ 64.
Bezug zum Lehrplan
In alltäglichen Situationen, vor allem bei der Begegnung mit Sachaufgaben, ist die Anwendung des halbschriftlichen Multiplizierens nötig.Beispiel:
Ein Tag hat 24 Stunden. Wie viele Stunden hat eine Woche?
oder:
Eine Breze kostet 67 Cent. Wie viel kosten 5 Brezen?
Beim Multiplizieren mit Geld muss darauf geachtet werden, dass die Benennung ( Preisangabe ) mit angeschrieben wird.
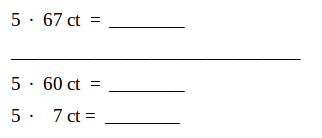
Im 4. Schuljahr erfolgt die Erweiterung auf den größeren Zahlenraum. Hier dient die Anwendung des halbschriftlichen Rechnens als Vorbereitung auf die schriftliche Multiplikation.
Beispiele für halbschriftliches Multiplizieren im größeren Zahlenraum:
An dieser Stelle muss auch das Kommutativgesetz (also: 4 ⋅ 527 = 527 ⋅ 4 )zur Anwendung kommen:
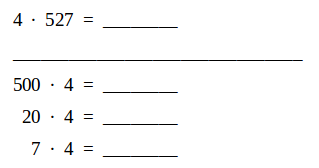
Die Bedeutung des halbschriftlichen Verfahrens bei der Multiplikation darf nicht unterschätzt werden. Es regt zum Erproben eigener Rechenwege oder zum Überprüfen von Strategien und Ergebnissen an und schult so das mathematische Denken.