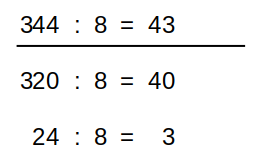Halbschriftliches Dividieren
Aufgaben und Übungen für Mathematik: Die Halbschriftliche Division
Voraussetzungen?
Strategien zum Lösen von Aufgaben mit dreistelligen bzw. noch größeren Dividenden
Bezug zum Lehrplan
Zu den Aufgabenblättern
Das halbschriftliche Dividieren durch einstellige Zahlen fällt den Kindern erheblich schwerer als das halbschriftliche Multiplizieren. Das liegt daran, dass der Dividend nicht so einfach in Hunderter, Zehner, Einer zerlegt werden kann wie beim Multiplizieren.
Die Hauptschwierigkeit für den Lernenden besteht darin, die geeignete Zerlegung des Dividenden zu finden.
Beispiel:
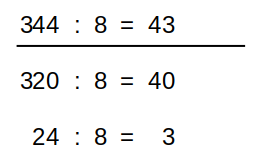
Voraussetzungen für das Lösen der Aufgaben
Hier gelten die gleichen Voraussetzungen wie für das Lösen halbschriftlicher Multiplikationsaufgaben:
- Kenntnis des kleinen Einmaleins und Einsdurcheins
- Kenntnis über die Vielfachen der Zehnerzahlen (Reihenbildung, z.B: 30, 60, 90, … oder 80, 160, 240, …)
- Ein schnelles Anwenden des Überschlagsrechnens hilft beim Lösen halbschriftlicher Aufgaben.
Beispiel:

Strategien zum Lösen von Aufgaben mit dreistelligen und noch größeren Dividenden
Zunächst sei hier betont, dass das halbschriftliche Dividieren sich in der Regel auf die Division durch einstellige Zahlen beschränkt.
Um halbschriftliche Divisionsaufgaben durchführen zu können, ist absolute Sicherheit im kleinen Einmaleins und Einsdurcheins nötig.
Beim halbschriftlichen Dividieren dreistelliger Zahlen können verschiedene Strategien angewandt werden.
Beispiel:

Beim Dividieren von dreistelligen Zahlen kann kaum auf zeichnerisches oder handelndes Tun zurückgegriffen werden. Hier muss gestütztes Kopfrechnen angewendet werden. Über das Nutzen operativer Beziehungen kann man oft zur richtigen Lösung gelangen.
Beispiel:

Im großen Zahlenraum, z.B. bis 10000, wird halbschriftliches Dividieren selten angewandt. In diesem Bereich ist Überschlagsrechnen sehr empfehlenswert, um vor dem Rechnen das Ergebnis abzuschätzen und nach dem Rechnen das Ergebnis zu kontrollieren.
Beispiel für halbschriftliches Dividieren:

Beispiel für Überschlagsrechnen:

Bei Aufgaben im großen Zahlenraum wird man aber rasch zur schriftlichen Division übergehen.
Bezug zum Lehrplan
Besonders nötig ist die Kenntnis des gestützten Kopfrechnens bei der halbschriftlichen Division im Zusammenhang mit einem sachrechnerischen Problem, z.B.:
Ein Lottogewinn von 330 € muss an drei Spieler gleichmäßig verteilt werden.
Vor allem beim Anstellen von Preisvergleichen im Alltag ist es von Vorteil, wenn das Kind halbschriftlich rechnen kann, z.B.:
Sechs Flaschen Mineralwasser kosten im Pack 1,92 €. Die Einzelflasche wird für 0,45 € angeboten. Vergleiche.
Die Schüler dürfen nicht zu früh auf eine Notationsform festgelegt werden. Sie sollen eigenständig Lösungswege entwickeln, Strategien nützen, verschiedene Rechenwege vergleichen und bewerten.
Welche Aufgaben müssen im 3., welche im 4. Schuljahr geleistet werden?
- 3. Schuljahr: Rechnen bis 1000, also z.B. 96:3= oder 966:3=
- 4. Schuljahr: Rechnen im großen Zahlenraum. Wie bereits erwähnt wird man hier schnell zum schriftlichen Rechnen übergehen.
Lehrgang "Halbschriftliches Dividieren"
Wir bieten vier Übungsblätter zum halbschriftlichen Dividieren an. Sie dürfen diese herunterladen, ausdrucken und im Rahmen unserer Nutzungsbedigungen verwenden.
Unsere Übungsblätter zum Thema:
Die Schüler werden zunächst eigene Rechenwege erproben und verschiedene Strategien anwenden, werden sich aber bald für einen für sie einsichtigen und vorteilhaften Weg entscheiden. Dadurch steigern sie ihr Vertrauen in ihre mathematischen Fähigkeiten.
Zu den Aufgabenblättern nach Jahrgangsstufe
Bitte wählen Sie die Jahrgangsstufe. Sie kommen zu den kostenlosen Aufgabenblättern und Lösungen.